


Next: Type III solar Radio
Up: Kinetic and Small Scale
Previous: MHD turbulence in the
Lecture 4 introduced two acceleration processes relevant to particles in
space plasmas: shock-drift acceleration involves particles undergoing plasma drifts
parallel or anti-parallel to the convection electric field, while diffusive shock
acceleration (or Fermi acceleration) involves particles being scattered back and forth
across a shock by magnetic turbulence. Evidence exists that each process is important at
some interplanetary shocks and it is sometimes difficult to either rule out one
process or to uniquely determine which process, if either, is
relevant to a given set of observations.
Figure 12.4 [Scholer et al., 1980; Smith, 1985, Fig. 4] compares the flux of energetic protons
observed during the passage of two CIRs near 4 AU.

Figure 12.4: Energetic protons associated with two CIRs are shown for one-half of a solar rotation
together with the associated profile of the magnetic field [Scholer et al., 1980; Smith, 1985].
The particle intensity shows maxima in the vicinity of the forward and reverse shocks with
minima near the peak field strength in each interaction region. The accelerated particles
extend both well upstream and downstream from the shocks.
While changes in flux are frequently
associated with the presence of a forward (F) or reverse (R) shock, there are
also more gradual changes. Mimima in the proton flux tend to be observed during times
of high magnetic field (and/or high levels of magnetic turbulence), associated with mirror
reflection and drifts away from the high field regions. This exclusion of energetic particles from
high field regions is responsible for ``Forbush'' decreases in the flux of cosmic rays,
as illustrated in Figure 12.5 for CIRs near 8 AU [Burlaga et al.,
1984; Smith, 1985]. (Note the merging together of most fast and slow streams,
but the retention of magnetic structures, by this distance.)

Figure 12.5: Voyager observations of cosmic rays at CIRs near 8 AU [Burlaga et al., 1984;
Smith, 1985]. The middle panel shows the ratio of the observed magnetic field strength
to that predicted for the Parker spiral model. The first two shocks are associated
with increases in the cosmic ray flux but followed by Forbush decreases in the high
field regions behind the shocks.
Shock-drift acceleration is predicted to be most effective for quasi-perpendicular shocks
(where the angle 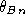 between the shock normal and field
between the shock normal and field  is close to 90 degrees)
with the energy gain being sensitively dependent on
is close to 90 degrees)
with the energy gain being sensitively dependent on 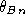 but restricted to factors
but restricted to factors
 . The requirement that
. The requirement that 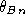 be
be  degrees means that the
accelerated particles will tend to be concentrated relatively close to the shock. Figure 12.6
illustrates this tendency.
degrees means that the
accelerated particles will tend to be concentrated relatively close to the shock. Figure 12.6
illustrates this tendency.
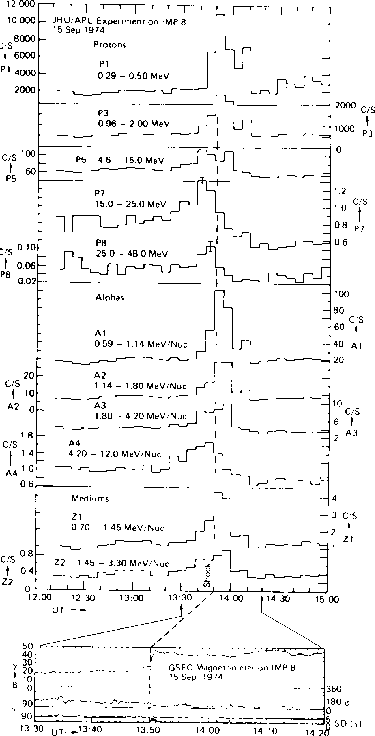
Figure 12.6: Count rates for protons, alpha particles and ``medium mass'' nuclei near an
almost perpendicular (  degrees)
transient interplanetary shock [Armstrong et al., 1985]. The peaking of the count rates
near the shock is consistent with shock drift acceleration.
degrees)
transient interplanetary shock [Armstrong et al., 1985]. The peaking of the count rates
near the shock is consistent with shock drift acceleration.
Diffusive shock acceleration can be important for both quasi-parallel and quasi-perpendicular
shocks. In the quasi-parallel case the accelerated particles and the waves they produce can
escape to large distances from the shock, thereby filling a large foreshock volume. Diffusive
shock acceleration tends to produce a power-law distribution with
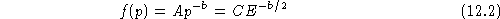
where b = 3 r/ (r -1) and 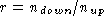 is the density jump across the
shock. For a strong shock (r = 4), then
is the density jump across the
shock. For a strong shock (r = 4), then 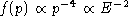 ; weaker shocks
produce steeper spectra. Diffusive acceleration also predicts an exponential increase in the
particle flux with decreasing distance to the shock. Figure 12.7 illustrates the predicted
power-law dependence of the distribution function downstream of a travelling interplanetary
shock [Gosling et al., 1981], while Figure 12.8 illustrates the expected exponential behaviour
of the count rate close to the shock [Scholer et al., 1983].
; weaker shocks
produce steeper spectra. Diffusive acceleration also predicts an exponential increase in the
particle flux with decreasing distance to the shock. Figure 12.7 illustrates the predicted
power-law dependence of the distribution function downstream of a travelling interplanetary
shock [Gosling et al., 1981], while Figure 12.8 illustrates the expected exponential behaviour
of the count rate close to the shock [Scholer et al., 1983].
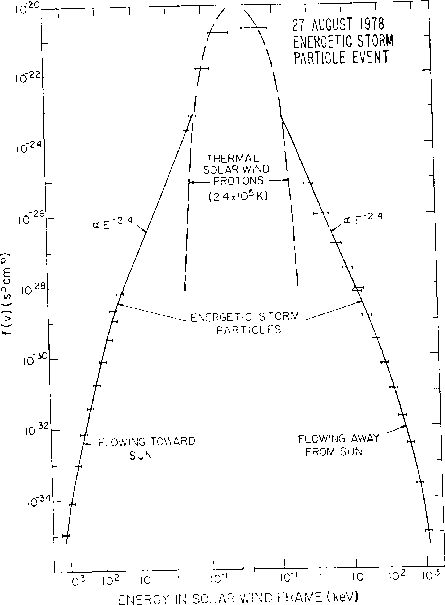
Figure 12.7: Measured distribution function of interplanetary protons in the solar wind
frame behind a transient interplanetary shock [Gosling et al., 1981; Scholer, 1985].
The distribution
is composed of a thermal core of solar wind protons plus superposed power law tails
consistent with diffusive shock acceleration.
MHD waves driven by the
accelerated particles have also been detected but are not discussed here. However, a detailed and
very successful application of diffusive shock acceleration to an interplanetary shock (addressing
both the waves and particles) is described by Kennel et al. [1984] and should be consulted by
interested readers.
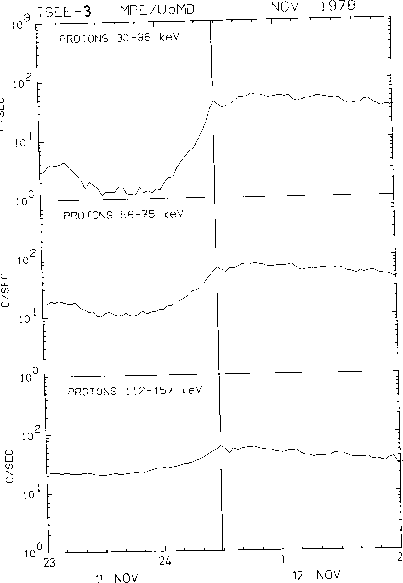
Figure 12.8: Exponential increases in the count rate of energetic particles with decreasing distance
to an interplanetary shock, qualitatively consistent with diffusive shock acceleration [Scholer
et al., 1983].



Next: Type III solar Radio
Up: Kinetic and Small Scale
Previous: MHD turbulence in the
Iver Cairns
Wed Sep 8 09:24:55 EST 1999




