The theory developed in Lecture 7 for the solar wind assumes a smooth, time invariant flow. In fact, the solar wind is a prime example of a medium with well developed, dynamically important turbulence . The term ``turbulence'' is used to describe small scale structures that cause the properties of the medium to vary in time and/or position with a large range of time scales. Turbulence is often but not always made up of multiple, broadband waves.
Belcher and Davis [1971] first demonstrated that the solar wind contains MHD turbulence: Figure 12.1 shows coupled variations in the three component's of the magnetic field and fluid velocity of the solar wind.
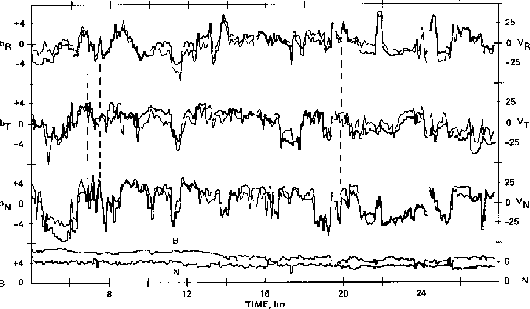
Figure 12.1: Alfven waves in the solar wind [Belcher and Davis, 1971]. The top
three panels each show a different orthogonal component of the solar wind magnetic
field and the associated (fluid) velocity component of the plasma. The bottom
panel displays the magnitudes of the total magnetic field and flow speed.
The correlation between the various components is very good and it should be noted that the total magnetic field strength and plasma density are essentially constant. Consistent with the theoretical properties derived in Lecture 3, these data are interpreted in terms of Alfven waves. (More recent investigations [e.g., Leamon et al., 1998] have also demonstrated the presence of components other than simple MHD wave modes in solar wind MHD turbulence.) In more detail, these waves primarily propagate outward from the Sun [Goldstein et al., 1995], suggesting a solar origin and possible connection with the heating of the corona.
MHD turbulence is usually investigated theoretically using the MHD equations. Statistical quantities are of primary use in understanding turbulence. Accordingly, correlation functions
where 
is a time lag, and their associated power spectra play a central role in both
theories and observations.
The primary quantitty considered is the power spectrum (or power spectral density), which is
calculated by Fourier transforming 
to yield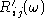 
and then forming
.
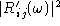Most turbulence theories involve the processes by which energy injected into a medium at large spatial scales is converted into motions at smaller and smaller spatial scales (or eddies) until reaching scales at which the turbulence energy interacts directly with individual plasma particles and causes heating (Figure 12.2).
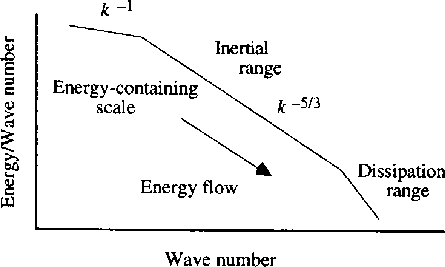
Figure 12.2: Schematic illustration of the power spectrum of MHD turbulence in
the solar wind [Goldstein et al., 1995].
The process by which wave energy moves to smaller wavenumbers is sometimes called a turbulent cascade. This process can be mimicked to some degree by stirring a fluid and watching it come into equilibrium. The range of wavenumbers over which the turbulence energy cascades to smaller wavenumbers is called the inertial range. Using both gasdynamic (GD) and MHD theory, it can be shown using energy balance arguments that the power spectrum in the inertial range should be a power law with spectral index in the range 3/2 - 5/3. Kinetic theory is required to understand the dissipation of the turbulence in the so-called ``dissipation range'' at small spatial scales. Very recently Leamon et al. [1998] first convincingly demonstrated the detection of the change in spectral index and wave properties expected in the dissipation range. Figure 12.3 shows both the inertial range and dissipation range of MHD turbulence in the solar wind for a characteristic period.
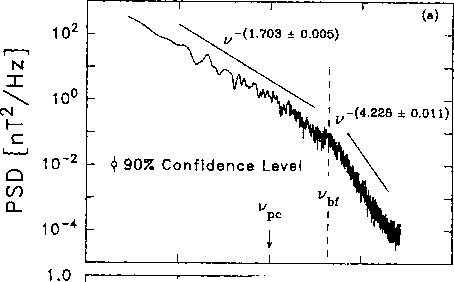
Figure 12.3: Typical spectrum of interplanetary magnetic field turbulence showing the
inertial and dissipation ranges [Leamon et al., 1998].
MHD turbulence is important for a number of reasons in space and solar physics. First, it accounts for many of the time and spatial variations in the fluid variables observed in the solar wind and other plasmas. Second, MHD turbulence is often vital in understanding the acceleration of particles at shocks, for instance in Fermi acceleration. Third, MHD turbulence can convert large scale fluid motions into heating of the thermal plasma. Fourth, generation of MHD turbulence can lead to the relaxation of unstable particle distributions, relevant to the discussions of comets and interstellar neutrals below. Finally, wave models for heating the solar corona often appeal to absorption of MHD turbulence. However, extrapolation of the power flux in solar wind MHD turbulence back to the corona does not remove existing difficulties in heating the corona [Goldstein et al., 1995].