Physics
of Baseball
1. The sweet spot
Batters know from experience that there is a sweet spot on the bat,
about 17 cm from the end of the barrel, where the shock of the impact, felt by the
hands, is reduced to such an extent that the batter is almost unaware of the
collision. At other impact points, the impact is usually felt as a sting or
jarring of the hands and forearm, particularly if the impact occurs at a point
well removed from the sweet spot.
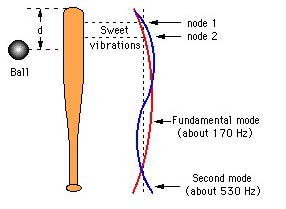
The sweet spot of a bat exists because bat vibrations
are not excited significantly at that spot. The spot is close to the centre of
percussion (COP) for a freely supported bat, so it was thought at one time that
the sweet spot might be associated with the COP. However, the COP shifts a long way toward the
handle when a batter holds the handle, and plays only a minor role in the feel
of the bat for an impact at the sweet spot.
These spots are described in the physics of tennis
page. A bat is similar to racquet but there are some obvious differences. For a
tennis racquet only the fundamental mode of vibration is excited by the impact
since the impact duration, about 5 msec, is too long to excite higher frequency
modes of the racquet. The impact on a baseball bat is shorter (since the bat
and ball are harder or stiffer), about 1 msec. As a result, the fundamental and
second vibration modes are both excited with about the same amplitude. These
modes are shown in the diagram above. Hence, there are two vibration nodes in
the barrel. An impact at the fundamental node will not excite that mode, but it
will excite the second mode. Similarly, an impact at the node of the second mode
will not excite the second mode but it will excite the fundamental mode.
Most people find that an impact at the node of the
fundamental mode feels best.
For further details, see American Journal of Physics,
September 1998 and also American Journal of Physics, 69,
231-232 (2001). The effect of the hands on the centre of percussion is
described in American Journal of Physics, 72, 622-630 (2004).
Alan Nathan has the world's best Physics of Baseball
site at www.npl.uiuc.edu/~a-nathan/pob/.
Another very interesting Physics of Baseball site is maintained by Dan Russell
at http://www.kettering.edu/~drussell
2.
Bounce of a baseball
The impact of a bat and a ball is still not properly
understood. A lot has been learned over the years but more experiments need to
be done to better understand how the ball bounces and how much spin it acquires
when it bounces. The flight of a
ball through the air depends strongly on how fast it spins, and in what
direction it spins.
The movie file below shows a baseball bouncing on low
pile carpet on the concrete floor in my office. The time between each frame is
0.040 seconds (25 frames/sec) and the ball is 72 mm in diameter. From that you
can work out the speed and spin of the ball before and after it bounces. In
principle you could also work out the acceleration due to gravity in Sydney,
but not very accurately.
The ball is spinning clockwise before it bounces and
hits the floor with backspin. The
ball bounces backward spinning counter-clockwise, then bounces again spinning
clockwise. The reversal of the spin each bounce implies that there is some
elastic behaviour in a direction parallel to the floor, either in the ball or
in the carpet, or both. There is obviously some elastic behaviour in the
vertical direction as well, which is why the ball bounces up off the floor.
Elastic behaviour in the vertical direction is described by a number called the
coefficient of restitution (COR) which is about 0.5 for a baseball, depending
slightly on ball speed. If the
ball didn't bounce at all then COR would be zero. If there was no loss of energy during the bounce then COR would
be 1.0
Elastic behaviour in the horizontal direction can be described
by a tangential coefficient of restitution, which is about 0.2 for a baseball
on wood at low ball speeds. It has never been measured for a baseball impacting
at high speed on wood. Alan Nathan and I published a paper about this in the
Oct 2006 issue of Am. J. Phys. (pp 896-904). The paper is available on Alan's
web site (see above).
Interesting information on the behaviour of a ball can
be obtained by bouncing it on a force plate or on a piezo to measure force vs
time. Typical results are shown here for a superball, a baseball and a
sorbothane ball. A superball has a COR of about 0.9, a baseball has a COR of
about 0.5 and a sorbothane ball has a COR of about 0.1 (ie it hardly bounces at
all). The shapes of the force vs time curves are interesting since they tell us
how the force on the ball varies with the amount of compression. Since F =
m*dv/t, we can integrate the force waveform to measure ball speed vs time, then
integrate v = dx/dt to measure the shift in the ball CM vs time.
The results show that F = kx for a superball or a
sorbothane ball, and F = k1*x +
k2*x^2 for a baseball, at least during the compression stage. As the ball
expands, the force drops more slowly with time, meaning that the ball suffers
some resistance to expansion. The results can be described by adding a damping
term proportional to dx/dt. The equation of the motion of the ball then has the
form
m*d^2x/dt^2 = -k1*x - k2*x^2 - Ax*dx/dt
where A is a constant that determines the amount of
damping and energy loss in the ball. If a ball has a large COR then A is small,
and vice-versa. This equation can be used to reproduce each of the force
waveforms shown below, and to
predict a COR value for each ball that agrees well with the observed
value.
Superball, 0.5 ms/div
Baseball, 0.2 ms/div
Sorbothane ball 2 ms/div
Graphs of F vs t and x vs t can also be used to
generate graphs of F vs x, showing how the force on the ball varies with its compression.
Results for a baseball dropped from heights of 1, 5, 10 and 15 cm onto a piezo
are shown below. The ball bounces while it is still compressed, and recovers to
its original sherical shape after it bounces.
3. Bat and ball collisions
The collision of a bat and a ball can be understood by
treating the bat as a heavy ball whose mass depends on the impact point. The
whole mass of the bat is not involved in the collision, unless the collision
happens to occur at the centre of mass of the bat. Otherwise, the effective
mass of the bat is less than its whole mass. To understand such collisions it
is important to first understand the physics of a collision between one ball
and another. Movies showing the collision
of a baseball with a cricket ball and the collision of two billiard balls are
shown in the page on collisions.
A hollow aluminum bat sounds a lot
different to a solid bat since the wall of a hollow bat can vibrate in and out like a drum.
Not exactly like a drum, more like a bell or a chime, but the effect is
similar. The sound made by a bat can be described as a "ping". The
frequency is typically between 1000 Hz and 2500 Hz, meaning that the wall
vibrates in and out 1000 to 2500 times in one second. The end result can be a
greater ball speed off the bat, in the same way that a tennis ball bounces a
lot better off tennis strings than off a hard floor. The effect is known as the
"trampoline effect". There is a difference between a bat and a
racquet here, in that tennis strings are very light and give back to the ball
95% of their stored elastic energy. The wall of a bat is relatively heavy and
returns only some of its stored elastic energy to the ball, keeping the rest to
itself so it can ping as loudly as it wants to. That is, a large fraction of
the stored elastic energy in the wall is retained as vibrational energy in the
bat. If the vibration frequency is less than about 1000 Hz, the end result is
that ball comes off the bat at a lower speed than off a wood bat of the same
weight and swing weight. For that reason, the walls of a hollow bat need to be
relatively stiff so they can vibrate at a frequency larger than 1000 Hz. Thick
walls are also needed to help prevent the walls dinting or cracking.
Some hoop mode sounds are recorded in the following
QuickTime Movies, using an aluminum bat and several aluminum tubes of various
diameters and wall thickness. The tubes were suspended by a length of string so
that they could vibrate for a long time without damping. It was found, by
measuring the frequencies of lots of aluminum tubes (see photo) that the frequency is directly
proportional to the wall thickness and inversely proportional to the tube
diameter squared. The stiffness of a cylinder was found to be roughly
proportional to its length x (wall thickness / diameter) squared (rather than
cubed, since the wall thickness is not negligible compared with the radius for
most of these tubes).
Cylinder 2 (500
Hz) Cylinder 3
(200 Hz)
5. A Physics of Baseball Project
The experiment described below would be an ideal project
on the physics of baseball, for any high school or University physics student.
There is enough physics in it to keep a PhD student busy for a few years, but it could also be done by any high
school student as a simple introduction to the physics of baseball.
The idea is to mount a bat as a pendulum and strike it
with a ball at various spots along the barrel. One question that can be
answered this way is "Where on the bat does the ball bounce best?" In
theory, the ball bounces best for an impact at the center of mass of the bat,
provided we can ignore bat vibrations. But the bat vibrates strongly for
impacts near the tip of the bat and near its center of mass. Energy is lost
during the collision if the bat vibrates. As a result, the bounce is relatively
weak at the tip and near the center of mass.
If the ball is also mounted as a pendulum, the experiment can also be performed in
reverse, by swinging the bat at a stationary ball. We can then ask a similar
question. Where on the bat is the ball struck with the greatest speed? A first
guess would be at the tip of the bat since the tip travels the fastest. But
strong vibrations are generated for impacts near the tip. Furthermore, the tip
is the lightest and least effective part of the bat.
By combining the results of these two separate
experiments, we can then work out what happens when a bat is swung at an
incoming ball. The outgoing speed of the ball is just the sum of the two
separate parts - the speed when the bat is at rest plus the speed when the ball
is at rest.
Some results for an Easton BK7 aluminum bat are shown
below in 13 movie files, each about 1 Mb. Also shown for comparison is a bounce
off a heavy block of granite so that the COR of the ball can be determined. For
small swings of a pendulum, the incoming and outgoing speed of the pendulum bob
is proportional to its horizontal displacement, so the relevant ball speed
ratios can be measured directly off the film with a ruler. The bat is 84 cm
long, and has a mass of 849 gram. Its center of mass is 52.6 cm from the knob
end. The bat was swung through an axis 143 mm from the knob end. Its moment of inertia about an axis
through its center of mass is 0.184 kg.m^2. The impacts were at distances of 2,
7, 12, 17, 24 and 31 cm from the end of the barrel.
Impact at 2 cm Impact at 7 cm Impact at 12 cm Impact at 17 cm
Impact at 24 cm Impact at 31 cm
Strike
at 2cm
Strike at 7 cm
Strike at 12 cm Strike at 17 cm Strike at 24 cm Strike at 31 cm.
The lines behind the bat, passing through the axis,
mark out angles of 5, 10, 15, 20, 25 and 30 degrees. The bat was swung through
an angle of about 30 degrees to strike the ball. Each impact was recorded on a
video camera at 25 frames/sec.
Coefficient of Restitution = Relative speed of bat and
ball after collision/ relative speed before collision, where "speed of
bat" is the speed of the bat at the impact point.
The COR for the impact on the granite block is about
0.59 in the low speed collision here, but can be as low as 0.45 in a 100 mph
collision. The COR for a collision between the bat and the ball is less than
0.59 when energy is lost to vibrations, but can be greater than 0.59 if the bat
has a trampoline effect on the ball. A high performance bat has a strong
trampoline effect and hence a relatively large COR. The technique here can be be used to measure the performance
of any bat, at least at low ball speeds. The swing weight of the bat (that
is, its moment of inertia) can be
determined from the measured period of oscillation when swung as a pendulum.
The bounce factor found from these and some additional
impacts is shown below.
The relevant collision equations are derived in The
Physics and Technology of Tennis book (and elsewhere) and are:
1. If the
bat is at rest then we can define the ball speed ratio
Bounce Factor = q = (ball exit speed) / (incident ball
speed)
q is also called the apparent coefficient of
restitution or ACOR. q varies from about zero near the tip of the bat to about
0.2 or 0.3 further along the barrel, and needs to be measured for any given bat
since it is usually too hard to calculate. So,
Ball exit speed = q*vin
where vin = incident ball speed.
2. If the ball is at rest (as in a tennis serve) then
Ball exit speed = (1 + q)V
where V = bat speed at impact point just before the
impact.
3. If the bat approaches a ball incident at speed vin
then
Ball exit speed = (1 + q)V + q*vin
The impact point 2 cm from the tip of the Easton bat is
a dead spot where the ball doesn't bounce at all, so q = 0. However, when the
bat strikes the ball at the dead spot then the ball exit speed = V = speed of
bat just before the collision.
6. Swing speed vs bat weight
Are heavy bats are more powerful than light bats? The
answer depends on how fast each bat can be swung. The following three movies
show a batter swinging three different bats as fast as possible, filmed at 25
frames/sec. One was a 232 gram
broomstick, one was a 871 gram Louisville Slugger wood bat with four holes
drilled through the barrel, and one was the 871 gram bat increased to 1333 gram
by inserting a steel bolt through each hole. The 232 g bat was swung at 45
radians/sec on average (by the batter in the film). The same batter swung the 871
g bat at 33 radians/sec on average, and he swung the 1333 g bat at 26
radians/sec on average. If you turn the volume up you will hear how the swing
speed affects the sound of the ÒswishÓ through the air.
232 g bat 871 g bat 1333
g bat
The above results are more or less as expected, in
that light bats can be swung faster than heavy bats. However, there are many variables in experiments
like these. It is not the actual weight that determines the swing speed but the
swing weight (ie the moment of inertia). In general, swing weight increases
with actual weight, but swing
weight also depends on bat length and weight distribution. The weight and
construction of a bat also affects the bounce factor q, and it affects the time
and position of the bat at which the swing speed is a maximum. The batter might
find that he needs to change the way he swings the bat if the swing weight is
altered, or he might have a ÒgroovedÓ swing technique and swing every bat the
same way. There is no simple physics answer to the heavy/light bat question
here.
A question that is equally interesting is how the
swing speed of each body segment varies as the bat speed varies and as the bat
swing weight varies. The shoulders reach maximum speed first, then the upper arms, then the forearm
and finally the bat. Any two connected segments can be analysed as a double
pendulum. The bat and the forearms are locked at right angles at the beginning
of the swing, by locking the wrists, otherwise the bat would start to rotate in
the wrong direction at the beginning of the swing. Near the end of the swing,
the bat swings so fast that the batter can no longer keep his wrists locked,
and the centripital force on the bat is about equal to the weight of the
batter.
7. Softball spin speed
It is not easy to find information on the actual rate
of spin of a softball in flight, but it is relatively easy to measure, at least
at low ball speeds and low spin speeds. I tossed a 12 inch softball at very low
speed and filmed the result, using two hands instead of one to increase the
spin rate and to make sure the spin axis was horizontal. The result was not a
super slow softball spin, neither was it particularly fast. I simply wanted to
know whether a hand launched ball spins at around 100 rpm or whether it could
be as high as 1000 rpm. The ball rotated more than 1/4 but less than 1/2 of one
revolution from one frame to the next, each frame being 0.04 sec apart. Taking
the rotation rate as 3/8 revolution / 0.04 sec gives 9.4 revolutions / sec or
560 rpm. It would therefore not be surprising if a softball can be pitched at
say 1000 rpm. A rough estimate would be that the ball rotates 1/4 revolution while
it is in the pitcherÕs hand, and
while the hand moves forward say the last
0.2 m. If the hand moves
forward at 10 m/s = 22.4 mph then
it moves 0.2 m in 0.02 sec, so the spin rate would be 12.5 rev/s or 750 rpm.
The hand moves forward faster than this in practice, so the spin rate could
easily be around 1500 rpm.
Another simple estimate of spin rate is to throw the
ball and catch it with the other hand as soon as it is released. The ball will
rotate about 1/2 a revolution from the initial grip to the release point, in
about 0.1 sec or less.
The film is shown here,
taken at 25 frames/sec.
8. How to swing a bat (June 2008)
It is not difficult to swing a bat. It is almost as
easy as walking. But how does a
batter do it? Specifically, what forces and torques are exerted on the handle,
and in what directions do they act?
It is very surprising that noone seems to have worked this out before.
Adair provides a few answers in his book ÒThe Physics of BaseballÓ but he does not give the directions or
the torques. The diagram below shows the swing of a wood bat filmed from a spot
above the batterÕs head. The force on the bat can be worked out from the
velocity of the center of mass, (CM), and the torques can be worked out from
the angular acceleration. The results are very surprising. Initially, the force
on the handle is in the opposite direction to the motion of the handle. While
the center of mass moves one way (nearly upward here), the handle moves the
opposite way (nearly downward). The batter needs to exert a small couple to get
the swing started, using equal and opposite forces on the handle, otherwise the
barrel of the bat will get left behind.
Near the end of the swing, the force is roughly at right angles to motion
of the handle since the centripetal force is very large. However, the
centripetal force does not act along the axis of the bat, but at an angle, as
shown by the orange lines.
The direction of the centripetal force is toward the
center of the circle followed by the path of the CM. Since the CM traces out a spiral rather than a circular
path, the center of the circle moves, as the bat is swung, along the path traced out by the inner
circle of black dots. At any given time, the center of the circle can be found
by fitting a circle to three neighboring points, at say time t, and at times
t+0.02 s and t-0.02 s. This gives the radius, R, of the circle, from which we
can calculate the centripetal force MV2/R as well as the force at right angles to that, given
by MdV/dt.
Near the end of the swing, the batter needs to exert a
large negative couple on the bat, otherwise the bat will swing around too fast
and strike the ball when it is aligned at the wrong angle. The same thing
happens when swinging a golf club, but it is not a well-known effect. Rather,
most coaches and others think in terms of wrist torque, which is probably much
too small to provide the necessary large couple near the end of the swing The
couple must come mainly from the two arms, not the wrists.
_______________________