Grand Slam Statistics

Rod Cross June 2009

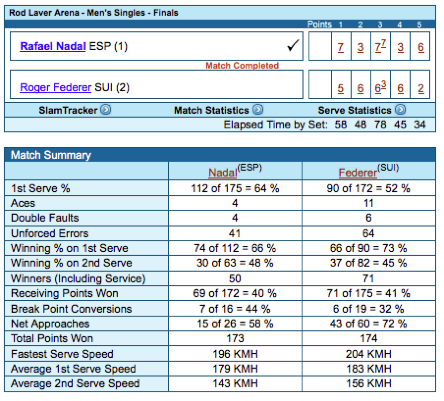
Each match played at each Grand Slam tournament has a Match Statistics summary on the web site, similar to the one shown here for the 2009 Australian Open men’s singles final. The numbers contain valuable information for both players and coaches. The numbers are also useful for statistics calculations.

As shown by the Nadal vs Federer example, the winner is not necessarily the one who won the most points or the most games. The winner is the one who won the important points and the important games and ended up with the most sets. In the long run, it makes no difference in a 5-set match if the player loses one of those sets 6-7 or 2-6, although it might temporarily dent his confidence to lose a set 0-6. Similarly, it makes no difference (other than to pride and confidence level) if the player loses a game to love or loses it after a few deuce points.

Definition of terms

1st Serve % = fraction of first serves that went in (the other first serves being a fault). Nadal served 175 first serves. 112 of those or 64% were good and the other 63 were faults.

Winning % on 1st Serve = fraction of good first serves won by the server. Nadal won 66% of his good 1st serves, or 74 out of 112.

Winning % on 2nd Serve = fraction of second serves won by the server (some of those serves being lost due to a double fault). Nadal won 48% or 30 of his 63 2nd serves.

Nadal won 74 + 30 = 104 points while he was serving, out of a possible 175, so he lost 71 points while he was serving. That’s why Federer won 71 out of 175 points when he was receiving.

Similarly, Nadal won 69 out of 172 points while he was receiving, so he won 104 + 69 = 173 points altogether.

Nadal had 16 opportunities to break Federer’s serve, and was successful on 7 occasions. He obviously tried hard to win those points and was successful 44% of the time. When he was receiving, he won only 40% of the time on average. On the other hand, Federer won 41% of the points when he was receiving, but he won only 32% of the time when he had a break point opportunity. Either he wasn’t trying hard enough, or he tried too hard and hit the ball out too often or Nadal decided that he wanted the point more than Federer wanted it. Whatever the case, Federer lost the match because he was unable to convert enough break points and because Nadal converted too many. A whole match can depend, in retrospect, on just one critical break point.

Probability of winning a point

The outcome of a match, in a statistical sense, depends to a large extent on the probability, p, that the server wins a point when he (or she) is serving. The formula for p is

p = fw + (1 - f) s

where f = 1st Serve %, w = Winning % on 1st Serve and s = Winning % on 2nd Serve

For Nadal, f = 0.64, w = 0.66 and s = 0.48 so p(Nadal) = 0.64 x 0.66 + 0.36 x 0.48 = 0.595. For Federer, f = 0.52, w = 0.73 and s = 0.45 so p(Federer) = 0.52 x 0.73 + 0.48 x 0.45 = 0.596. Both players had an essentially equal chance of winning a point when they were serving, so that had an equal chance of winning (or losing) a game when they were serving. Federer had a bad serving day. He won 73% of his first serves when they went in, but he got only 52% of them in.

For any given match, the point probability, p, of the server winning a point can also be calculated from the total number of service points won by each player. For example, suppose that player A wins W1 of his N1 good first serves during the whole match and also wins W2 of his N2 second serves. Then

p(A) = (W1 + W2)/(N1 + N2)

f = N1/(N1 + N2), w = W1/N1 and s = W2/N2.

Probability of winning a game

How many times did Nadal step up to serve, and how many times did he win the game when he was serving? We can work this out from the Table. The total number of games in the match, from the set score, was 50, not counting the tie-break game. So they each stepped up to serve 25 times. Federer broke Nadal’s serve 6 times (the 6 conversions) and Nadal broke Federer’s serve 7 times (his 7 conversions). Nadal won 25 games in total (not counting the tie break game), so he won 18 of his own service games plus the 7 games he won when he broke Federer’s serve. Federer also won 25 games, so he won 19 of his own service games plus the 6 he won when he broke Nadal’s serve. Nadal’s chance of winning one of his own service games was therefore 18/25 = 0.72, while Federer’s chance was 19/25 = 0.76. Nadal won the same number of games as Federer by winning the tie-break game.

Grand Slam Parameters

Every match is described by a different set of parameters for each winner and loser. I looked at each of four Grand Slam tournaments (in 2008 and 2009) and at the last 31 matches in each tournament from Round 3 to the final. The average values for each tournament, for both men and women singles, are shown in Table 1, where A = winner and B = loser of each match.

g = probability of server winning his or her serve game.

r = 1 - p = probability of server losing a point when serving = probability of the receiver winning the point.

C = Break Point Conversion % = fraction or percentage of break point opportunities won (converted) by the receiver.

TB = fraction of sets that end in a tie break.

Table 1 lists average quantities, averaged over the N winners and the N losers of each match. For women, N was 31 for the French Open and Wimbledon, 28 at the Australian Open (since three of the matches were not completed) and 30 at the US Open since the statistics were not correctly recorded in one match.

Some observations from this table are as follows:

The 1st Serve % (f) is about 0.62 at all tournaments for both winners and losers, for both men and women. Men at the Australian Open averaged 0.67 in 2009.

Winning women players win about 70% of their good 1st serves at all 4 tournaments (wA ~ 0.70), while losing players win only about 58% of their good 1st serves (wB ~ 0.58). Men do better, with wA ~ 0.78 and wB ~ 0.66.

Winning women players win about 50% of their 2nd serves at all 4 tournaments (sA ~ 0.50), while losing players win only about 40% of their 2nd serves (sB ~ 0.40). Men do better, with sA ~ 0.57 and sB ~ 0.47.

The probability of winning a point when serving is about 0.62 for women winners at all 4 tournaments (pA ~ 0.62), and about 0.50 for losers. Men do better, with pA ~ 0.70 and pB ~ 0.58.

The probability of the server winning a game (when serving) is about 0.80 for women winners at all 4 tournaments (gA ~ 0.80), and about 0.50 for losers, although both figures are higher at Wimbledon and lower at the French Open, especially for the loser. The losing woman player can expect to lose serve more than half the time at the French Open, and about half the time at the Australian and US Open. For men, gA ~ 0.90 and gB ~ 0.68. The serve is more dominant in the men's game.

The winning woman player can expect to win about half the points when receiving serve (rA ~ 0.5), but the losing player wins only about 37% of the points on average when receiving (rB ~ 0.37). For men, rA ~ 0.40 and rB ~ 0.30, with the result that there are fewer break point opportunities.

The chance of converting a break point is about the same as winning any other point when receiving, when averaged over all players, and is especially difficult for the losing player at Wimbledon where CB = 0.285 for women and CB = 0.225 for men. In any individual match, C can be quite different to r. A break point is a critical point. Some players handle it better than others and actually win a greater fraction of their break points than any other point, while some players wilt under the pressure (or are just unlucky) and are less successful when they face a break point.

Probability of winning a game.

Since p = probability of winning a point, p x p is the probability of winning two points in a row when serving, 1-p = probability of losing a point, and (1-p) x (1- p) is the probability of losing two points in a row. For example, if p = 0.6, then the server can expect to win two points in a row 36% of the time, he can expect to lose two points in a row 16% of the time, and he can expect to win then lose a point or lose then win a point 2 x 0.6 x 0.4 = 48% of the time. The chance of winning 4 points in a row is 0.6 x 0.6 x 0.6 x 0.6 = 0.13, so the server can expect to win a game to love 13 % of the time, and can expect to lose a game to love 2.6% of the time.

Extending this process to consider all possible outcomes, we can work out the probability, g, of winning a game, and the answer (including deuce games) is

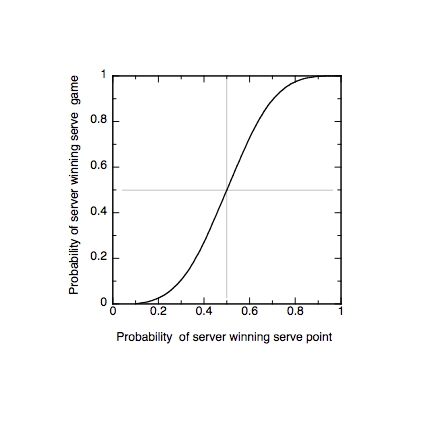
A graph of g vs p follows, showing that if p = 0.5 then g = 0.5 and that the probability of the server winning the game increases rapidly with only a small increase in p. For example, if p = 0.7 then g = 0.90. The probability of the server winning a point depends on how well he or she is serving and on the ability of the opponent.

Knowing the probability that player A wins his service game, and the probability that player B wins his service game, we can calculate the most likely outcome of the set and the probability that player A wins 6-0 or 6-1 etc or loses by these various set scores. Some results are shown below. There are some surprises. For example if pA = 0.6 and pB = 0.6 then both players are evenly matched. The various possible outcomes are shown by the blue points, assuming that player A serves first. It is then more likely that player A will win 6-1 than lose 1-6, and it is more likely that he will lose 4-6 than win 6-4. The reason is that a 6-4 result can be obtained if player A loses none of his serves or loses up to 4 of his serves, while a 4-6 result can be obtained if player A loses up to 5 of his serves (while B wins 1 serve and loses 4). That is, there are more ways to lose than to win.

If pA = 0.6 and pB = 0.7 then the most likely result is that A loses 4-6, but there is also a small chance that A will win the set. At least, that is the case if every point is won or lost with the same probability. If player A absolutely refuses to concede a break point, or if player B is unable to break serve, then player A will win the set. Table 1 shows that the probability of winning a break point is not necessarily the same as winning other points. In some matches, C can be double or half the value of r, meaning that the player wins or loses twice as many break points as would normally be expected.