Figure 13.4 demonstrates that Earth's bow shock is a fast mode shock.
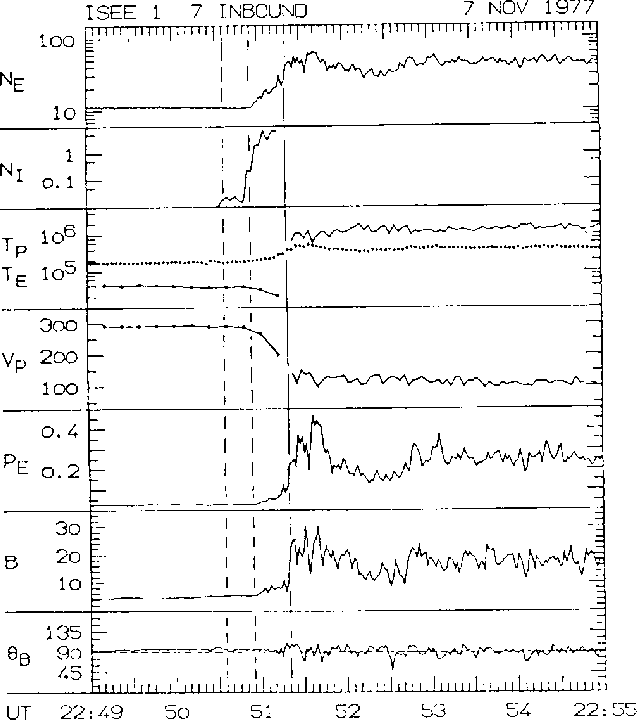
Figure 13.4: Crossing of Earth's bow shock in a region where the shock is quasi-perpendicular
and supercritical [Schopke et al., 1983]. The figure demonstrates that Earth's bow
shock is a
fast mode shock, as well as showing the presence of gyrating ions in the shock's foot.
Why? Because the plasma is slowed, heated, compressed (ruling
out an intermediate/Alfven shock), and the magnetic field is increased
in strength and changed in direction (ruling out a slow mode shock).
The deflection of the flow in velocity is also important, since it is
the first step in deflecting the flow around the magnetosphere. Note the
small spatial scale of the shock ramp - data similar to Figure 13.4
demonstrate that the spatial scale is of order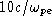 
,
corresponding to about 20 km and approximately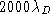 
.
Figure 13.5 shows the data for two other crossings of Earth's bow shock, while Figure 13.6 compares the fluid variables with the predictions of the MHD Rankine-Hugoniot conditions, accomplished by nonlinear least-squares fitting of the observations to the theory in order to determine the normal direction and other characteristics of the shock [e.g., Lepidi et al., 1997].
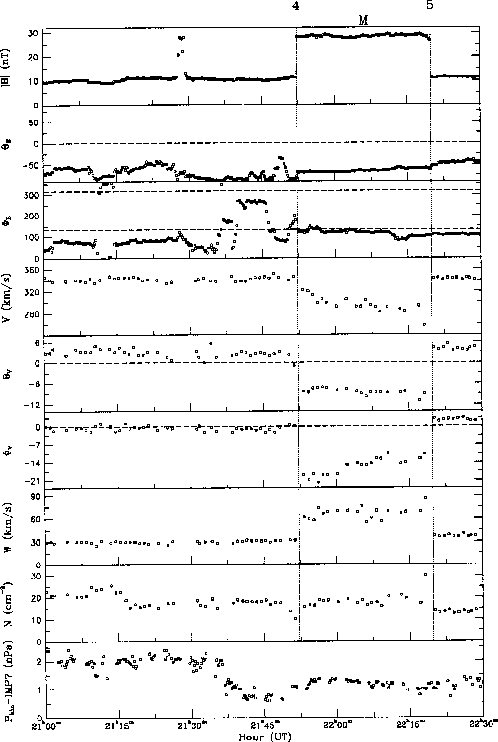
Figure 13.5: Traversal of Earth's bow shock into the solar wind with a subsequent
return into the magnetosheath [Lepidi et al., 1997].
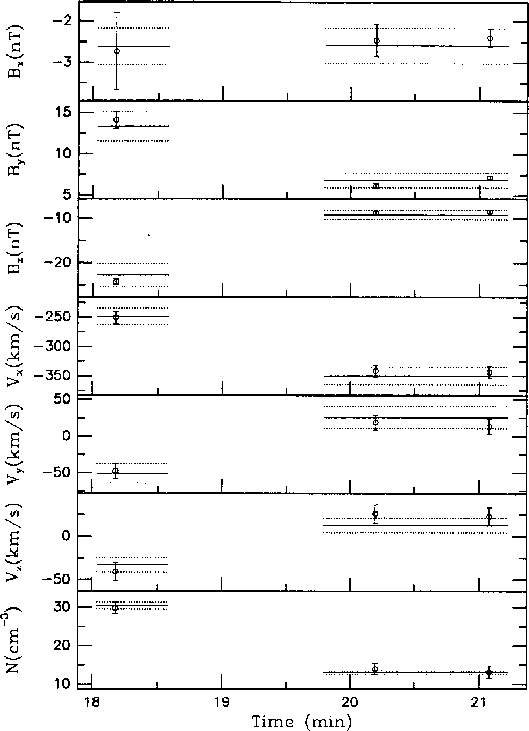
Figure 13.6: Comparison of observational data (open symbols with error bars) for the first
shock crossing in Figure 13.5 with predictions based on the Rankine-Hugoniot
conditions (solid lines with dashed lines showing the uncertainty limits)
[Lepidi et al., 1997].
As can be seen, the observations agree well with the theory.
The first indication that the MHD picture is too simple is apparent
when one considers the shock heating of the ions and electrons separately.
One finds that approximately 90% of the shock heating goes into the ions,
with only about 10% going into the electrons, resulting in the condition
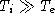being satisfied downstream from the shock. Second, most
of the ion heating is perpendicular to the magnetic field and is much
larger than the heating expected just from conservation of the first
adiabatic invariant across the shock's magnetic ramp. Third, the
electron heating is primarily consistent with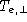 
increasing
adiabatically across the shock (i.e., constancy of the first adiabatic
invariant).
Consider now: ``How is the plasma temperature increased in a collisionless shock?''. The answer is easy for a collisional shock: collisions re-distribute the incoming ram kinetic energy as thermal energy. (This explains qualitatively the increase in downstream pressure being proportional to the Mach number squared in the gasdynamic shock in Question 2 of Assignment 2.) But how is this done in a collisionless shock? Not by Coulomb collisions (Assignment 1). As suggested by the temperature properties described above, the answer is partially by wave-particle scattering and other kinetic processes that are not included in fluid theories and partially by effects contained in two-fluid theory but not in MHD.